1: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:17:23.04 0.net
���Ѹ�: http://hayabusa3.2ch.sc/test/read.cgi/morningcoffee/1612772243/
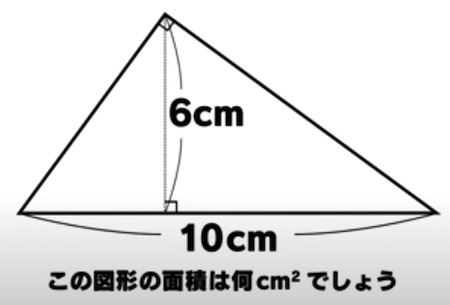
�������ա����С��������ݤ���
27: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:30:35.45 0.net
>>1 ĺ�����̤�ߤ��Ⱦ�¤�5cm
���־��ĺ������ߤ��濴(10cm���դ�����)�������ʬ��5cm�Ȥʤ�
���־��ĺ������10cm���դ˲�������������5cm���Ĺ���ʤ뤳�ȤϤʤ�
31: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:32:19.99 0.net
>>27 ĺ����3�����Ƥ�ĺ���Τ���
39: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:35:24.93 0.net
>>31 ���ѷ������Ƥ�ĺ�����̤�ߤäƤɤ�ʻ��ѷ��Ǥ���ΤʤΡ�
47: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:37:24.59 0.net
>>39 �Ƥ�3���ؼ����ʤ��ȱߤ������ʤ����顡2���������ȱߤ��礭������ޤ�ʤ�
52: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:40:04.60 0.net
>>39 ���ѷ������Ƥ�ĺ�����̤�ߤκ����ˡ��
���դο�ľ����ʬ���θ���������ɤ�ʻ��ѷ��Ǥ��Ϥ�����
3: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:18:11.10 0.net
�ɤ��ְ㤨���
4: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:18:54.55 0.net
1%���ְ㤨���ʤ�狼�뤱��
5: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:19:05.11 0.net
30����ͤ��Ρ�
6: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:19:46.74 0.net
��äѤ�ʬ���äƤʤ��ʣ�����
7: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:19:51.56 0.net
�ְ㤨�褦���ʤ�����
�Ф��Ⱦʬ�Ϻ���Ǥ⣵���������
������ʤ�Ƽ¸��Բ�ǽ����
8: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:20:23.32 0.net
����ʻ��ѷ���¸�ߤ��ʤ�
9: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:21:38.44 0.net
�ʤ�������ʤ�Τ��������´�����
10: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:21:51.68 0.net
�ʤ��ʤ������
11: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:22:20.46 0.net
���꤬�ְ�äƤ�Τ���
12: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:22:49.77 0.net
���ޤ��⤷�Ƥ���
16: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:26:10.50 0.net
>>12 ���դ�����Ⱦʬ�ΤȤ����˸�����ĺ����������������餽��Ĺ����5cm
23: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:28:26.18 0.net
>>16 �ʤ��5cm�ʤΤ���ʬ����ʤ�
13: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:23:17.21 0.net
���꤬�ְ㤤�ʤ��������ͤ��Ρ�
14: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:24:13.52 0.net
���ѷ������Ѥ���ʤ���
�������ѤäƽƤ���Τ������ط����롩
15: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:25:12.61 0.net
�⤵��6cm�Ϥ��ꤨ�ʤ�������äݤ�
17: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:26:16.03 0.net
��ͳ��ʬ����ʤ�
18: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:26:51.86 0.net
60��
19: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:27:10.32 0.net
����Υߥ��ץ������Ψ100�����
20: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:27:32.25 0.net
1��2����3
21: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:27:38.38 0.net
30
22: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:27:40.91 0.net
�����ɤ��Ǥ��컰�ѷ��Ǥ���6cm�褳10cm�ȽƤ���ʤ�30cm2�������ʳ��ʤ�����
24: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:29:18.26 0.net
10cm��ľ�¤Ȥ���ߤ�Ƥߤ��6cm�����������Τ�����ʬ����
25: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:29:30.93 0.net
CAD�ǽƤߤ�w
28: ̵̾���Υ˥塼®������ƥ����� 2021/02/08(��) 17:30:42.69 0.net
�구��Ȥ�











�����Ȥ����